Problem
Below we will define an n-interesting polygon. Your task is to find the area of a polygon for a given n.
A 1-interesting polygon is just a square with a side of length 1. An n-interesting polygon is obtained by taking the n - 1-interesting polygon and appending 1-interesting polygons to its rim, side by side. You can see the 1-, 2-, 3- and 4-interesting polygons in the picture below.
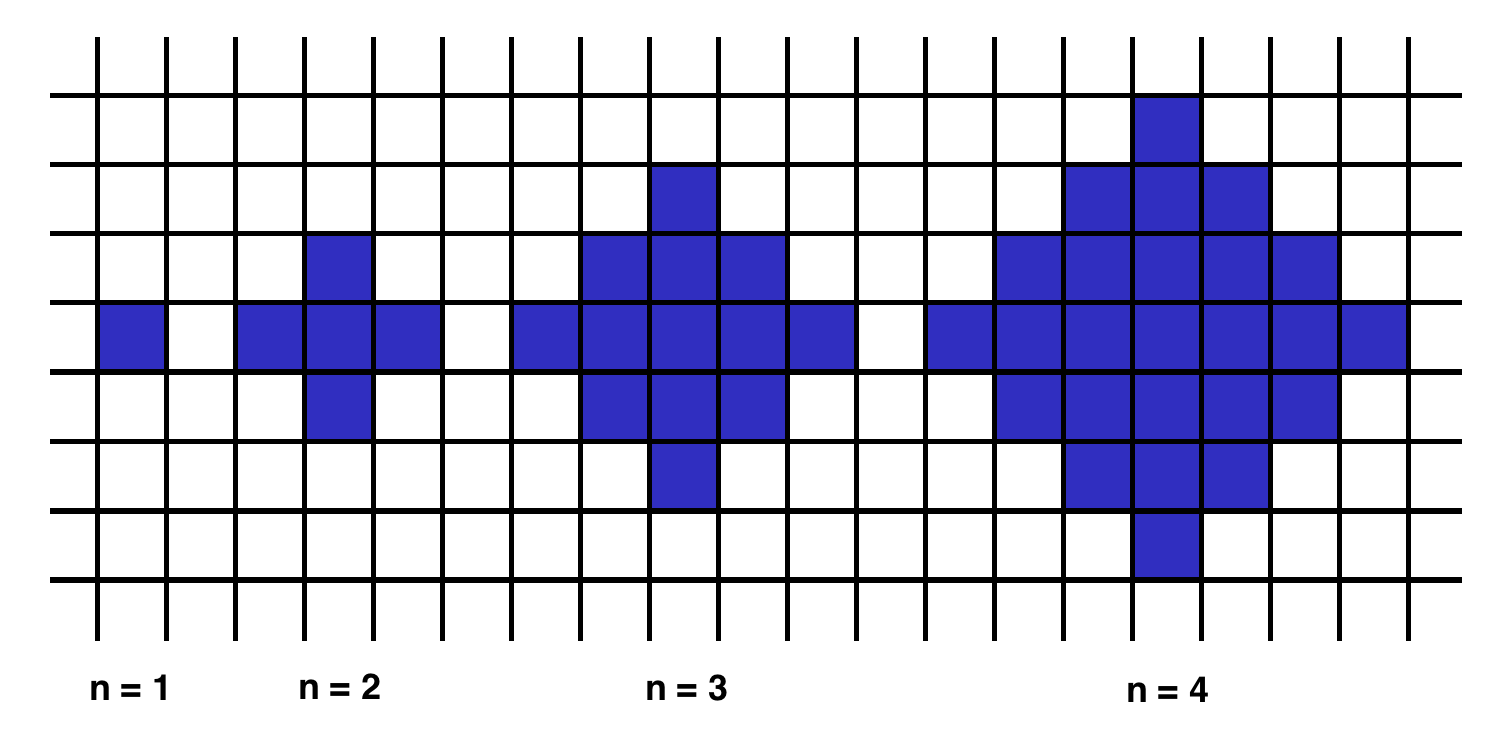
Example
- For
n = 2, the output should beshapeArea(n) = 5; - For
n = 3, the output should beshapeArea(n) = 13.
Input/Output
[input] integer n
Guaranteed constraints:
1 ≤ n < 104.[output] integer
The area of the
n-interesting polygon.
Solution
위의 그림과 같이 변화하는 도형의 개수를 예측하는 알고리즘 문제입니다.
이번 문제는 해당 알고리즘의 규칙만 찾으면 되는 단순한 문제입니다.
도형을 구성하는 사각형의 개수가 1개, 5개, 13개, 25개 ··· 와 같이 증가하고 있습니다.
이를 수식으로 표현하면 n의 제곱 + (n-1)의 제곱으로 표현할 수 있습니다.
'Programming > Algorithm' 카테고리의 다른 글
| [Algorithm] almostIncreasingSequence (0) | 2018.02.08 |
|---|---|
| [Algorithm] makeArrayConsecutive2 (0) | 2018.02.08 |
| [Algorithm] adjacentElementsProduct (0) | 2018.02.08 |
| [Algorithm] checkPalindrome (0) | 2018.02.07 |
| [Algorithm] centuryFromYear (0) | 2018.02.07 |